Is every group a symmetry group?
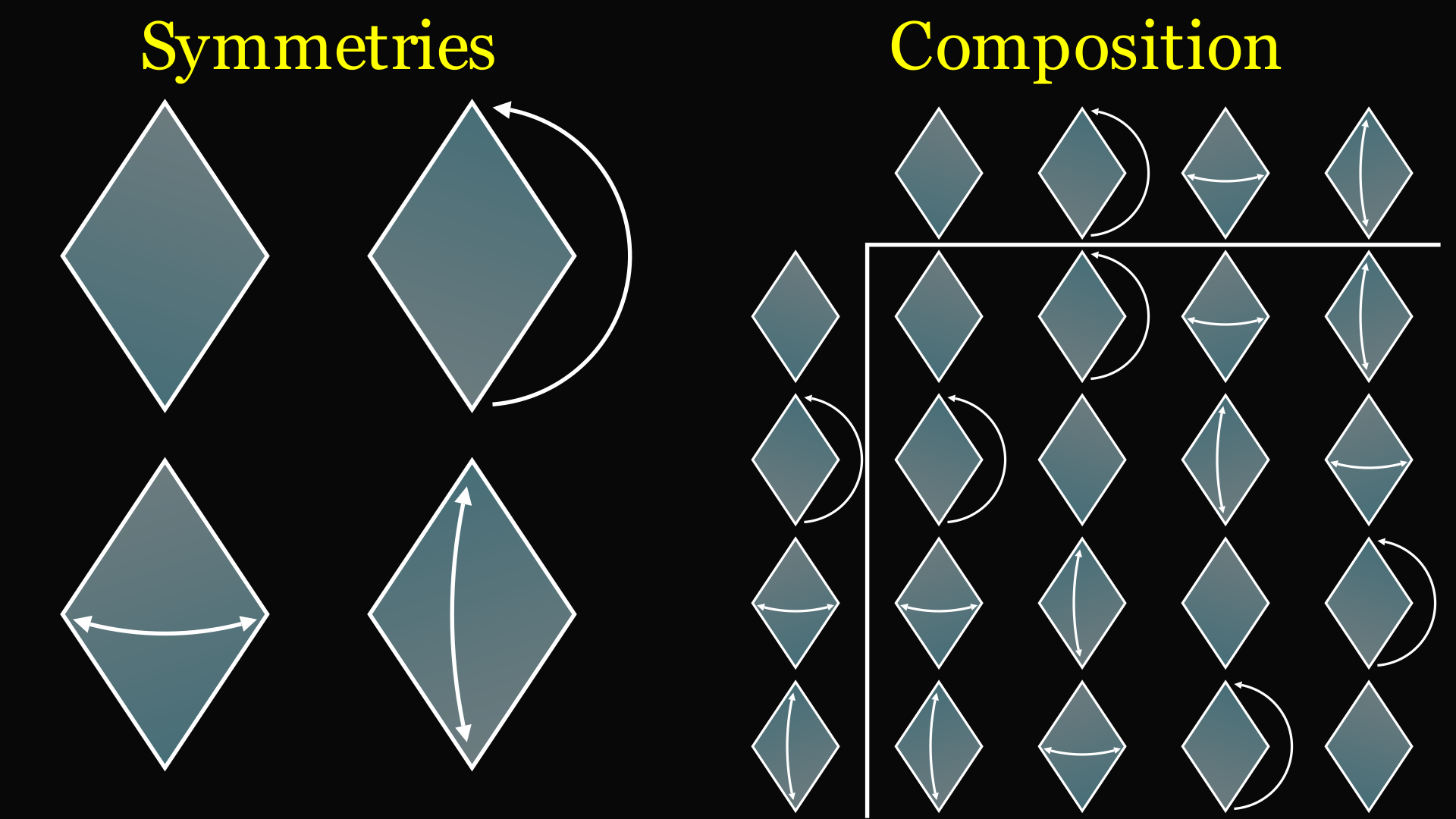
Groups are abstract mathematical objects. Because they are so general, they can be hard to visualize. For that reason, when you were introduced to groups, you were probably told that they represent the symmetries of an object. There are a bunch of actions you can take on the shape that leave it looking the same, symmetries, and doing them one after another, composing them, leads to a special structure called a group.

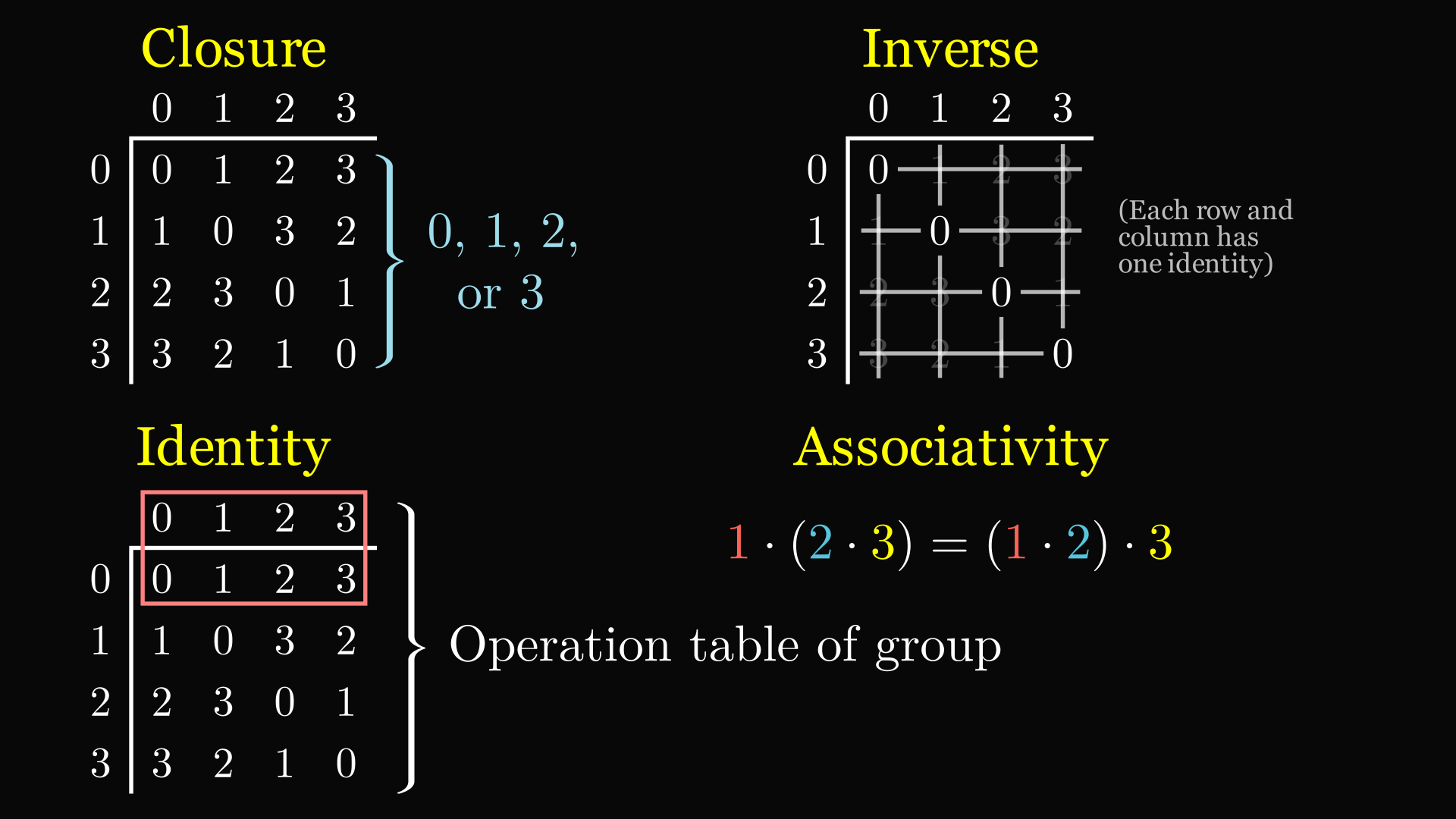
Later, you were probably told that a group is more generally any set which has an operation with four special properties: closure, identity, inverse, and associativity. The group is only defined by its operation table; the symbols in it don’t necessarily have their usual meaning, not even “multiplication”.
So can every group be represented by the symmetries of an object? That would be a much more concrete and easier way to visualize the group. This question actually leads straight into representation theory, a way to represent abstract concepts like groups with easier concepts like matrices.
First, why do the symmetries of an object make a group? The set of symmetries of an object are all of the transformations of space of some type, usually isometries, that leave the object looking the same. The group operation is the result of composing two transformations: doing them one after another. It’s important to realize that the elements of the group are movements of the object, not orientations.

If you do something that makes the object look the same, and then another thing that makes it look the same, it’s going to look the same. Doing them one after another is a symmetry, too. That’s closure.
You can do nothing, and nothing happens to the object, so it looks the same. So doing nothing is a symmetry. That's identity.
If you do something and the action is unchanged, then if you do it in reverse, the object is still unchanged. The reverse is a symmetry, too. That's the inverse.
And finally, it doesn't matter if you group two actions in a longer sequence into a single step: the sequence still has the same actions in the same order. That’s associativity.
These kinds of groups are called symmetry groups. Our question is: is any finite group G the symmetry group of some object, say a polytope? The answer is yes, and we can show two different ways to do it.
We want to map every element of the group to a way to move the object. For the mapping to be useful, we want it to actually describe the structure of the group. That means that the group operation should do the same thing whether applied to the group elements, or their physical realizations. It’s a group homomorphism from the group to the group of all transformations of the object.
Second, we want the movements of the object to actually be symmetries of the object. Those two criteria make the object a representation of the group. Or more technically, the subgroup of the general linear group corresponding to the symmetries of the object is a representation of the group, but we won’t worry about that.
We also want two distinct elements of the group to do different things to the object. Otherwise we can just say that every element of the group is the identity transformation of the object, which isn’t very useful. This makes the representation faithful, and the mapping between the groups an isomorphism. To make the object a perfect representation of the group, there should be no extra symmetries of the object that aren’t accounted for in the group. Otherwise we can just take a sphere of sufficiently high dimension, which isn’t very interesting, and won’t help you to visualize the group.
So we want to find an object whose symmetry group is isomorphic to the group in question. If the object is too symmetric, we can break some of its symmetries. For instance, we can break some of the symmetries of the square by squishing it into a rhombus. The symmetry group of the rhombus is then a subgroup of that of the square.

You might guess that we can’t describe every possible finite group with just the symmetries of 3-dimensional space. There are some big, complicated groups out there. So we will need to use polytopes of higher dimensions in order to describe more complicated groups. To keep things simple, we should use the n-dimensional object with the simplest symmetries, the n-simplex.
The symmetry group of a simplex is relatively large. Since all of the vertices are identical, and there are edges going between any two vertices, there is a transformation for any permutation, or rearrangement, of the vertices. The group of all permutations under composition is called a symmetric group, not to be confused with the symmetry groups from earlier. The symmetry group of a simplex with n vertices is the n-symmetric group.
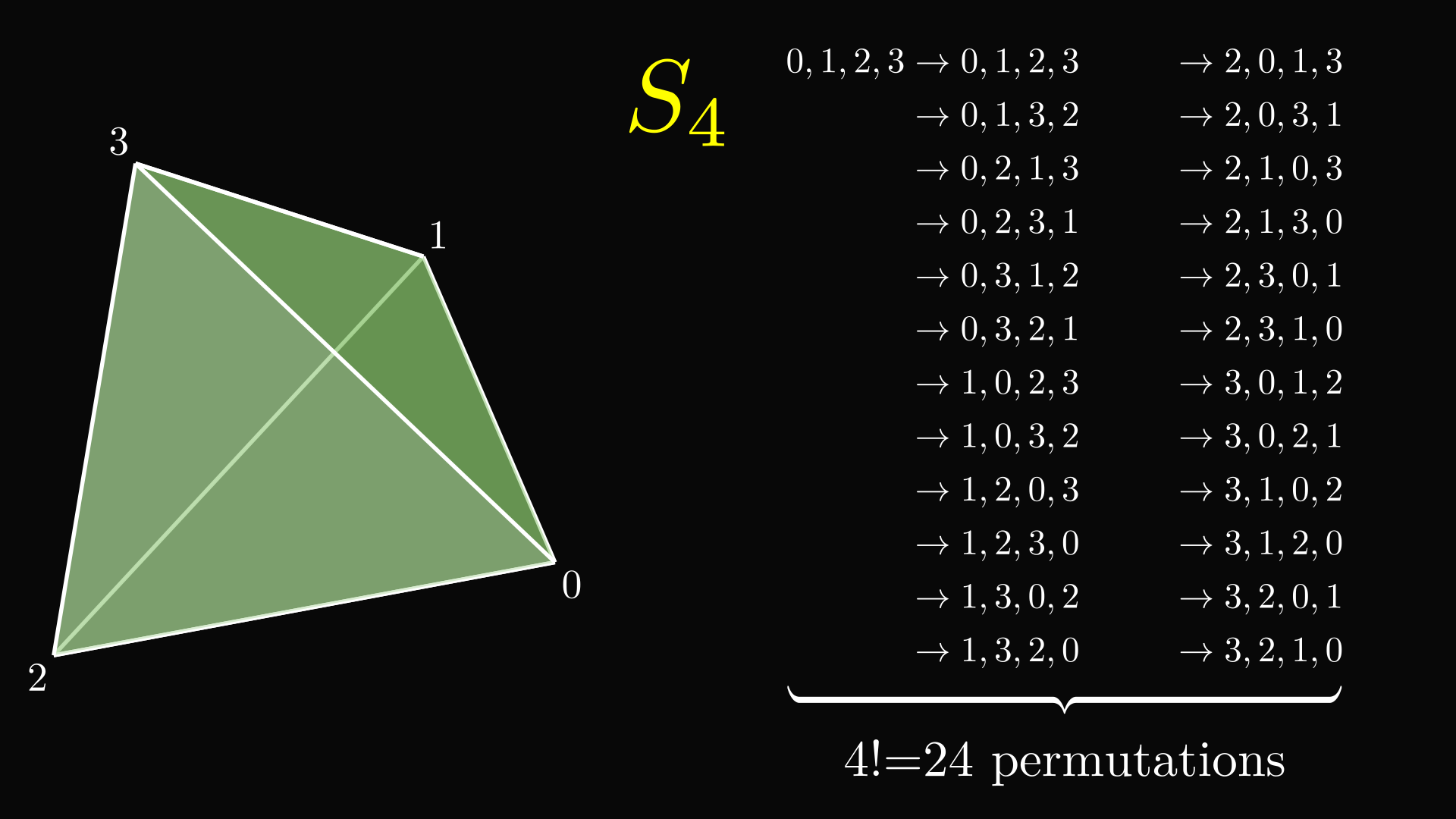
There is actually a very simple representation of the group using symmetric groups. Cayley’s theorem says that every group is a subgroup of the symmetric group of its own elements. In other words, you can destroy some symmetries of some symmetric group to get any group.
A subgroup of the n-symmetric group is a set of permutations, where when you compose any two permutations from the set, you get a permutation from the set. In other words, a subset of the symmetric group is what you get if you don’t allow some sorts of permutations, but still keep the group properties.
The set of permutations you’ll need is actually very simple if you look at the operation table of the group. Take a moment to think about how.

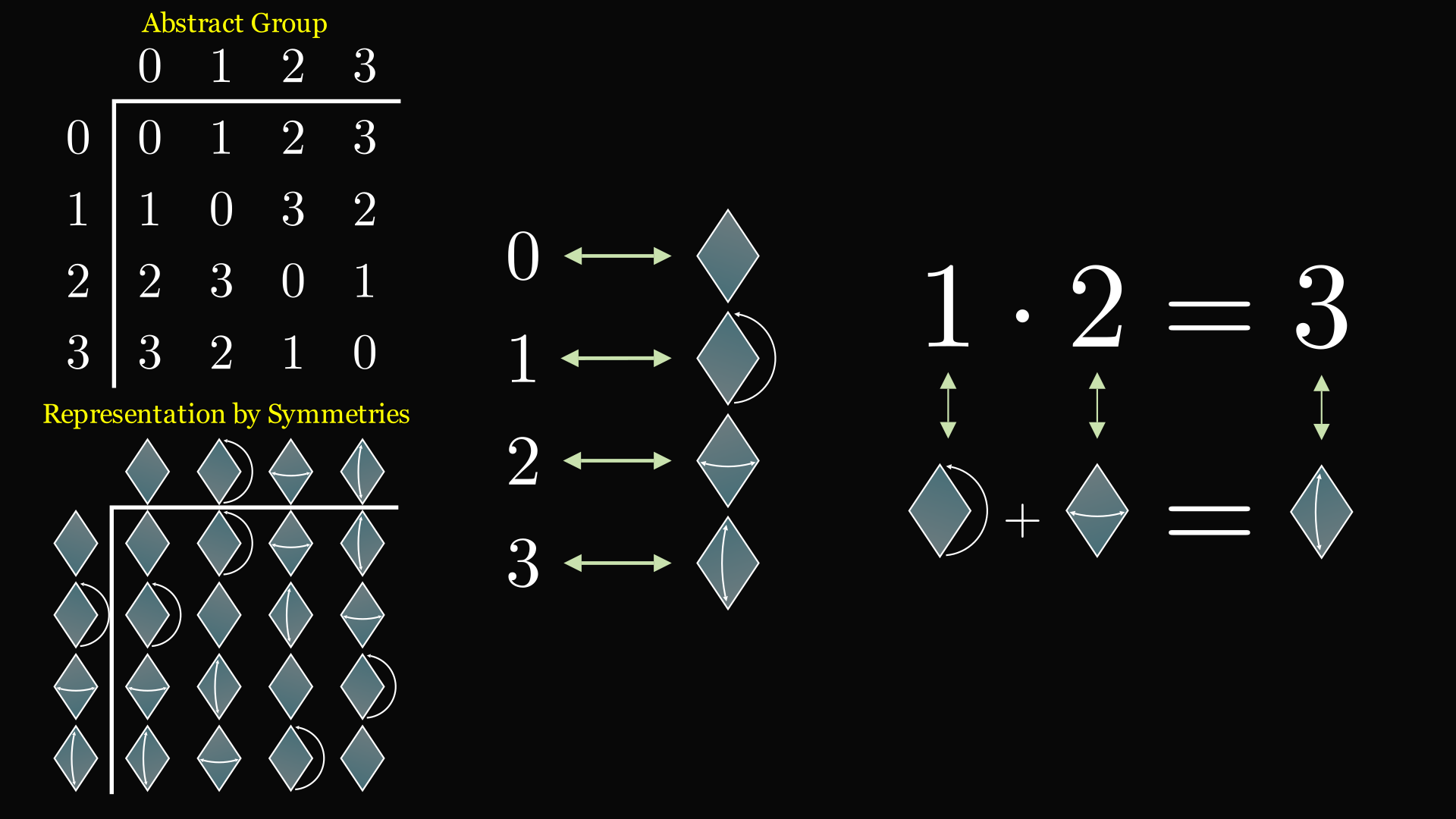
Notice how each element shuffles the other elements of the group. Imagine multiplying each element of the group by 3. All of the elements are listed on the top of the table. Multiplying by 3 (from the left) corresponds to looking at the 3 row of the table. The elements in that row have been shuffled: 0 swapped with 3 and 1 swapped with 2. Each element has to be represented exactly once in each row because of the ability to take inverses, so these are indeed permutations. These permutations can actually represent the group. This is how:
The operation of the group has to match the composition operation of the permutations. If the first permutation takes c to bc, and the second takes bc to abc, then the total effect is taking c to abc, a multiplication by ab. This means the composition of the permutations corresponding to a and b is the permutation corresponding to ab. Composition of the permutations and the group operation basically have the same effect, so this is a group homomorphism.
And that's the proof of Cayley's theorem! It is surprisingly simple, tumbling straight out of the operation table.
Now we can apply Cayley’s theorem to construct a polytope with any group G as a symmetry group. Since the symmetry group of the (n-1)-simplex is the n-symmetric group, inspired by Cayley’s theorem, we assign each vertex to an element of the group. Then each element of the group also corresponds to the transformation that permutes the vertices, like they were being multiplied by that element.

Each element a of the group corresponds to the transformation taking the vertex labeled b to the old location of the vertex labeled ab. This is a symmetry of the tetrahedron because all of the vertices and edges are identical. The only problem is that all of the other symmetries of the object are still valid. There are symmetries of the tetrahedron that don’t correspond to any group member. The tetrahedron is still a faithful representation of the group, it just would be nice if it didn’t have any of those extra symmetries. To make the representation better, we need to destroy some of the symmetries of the object.
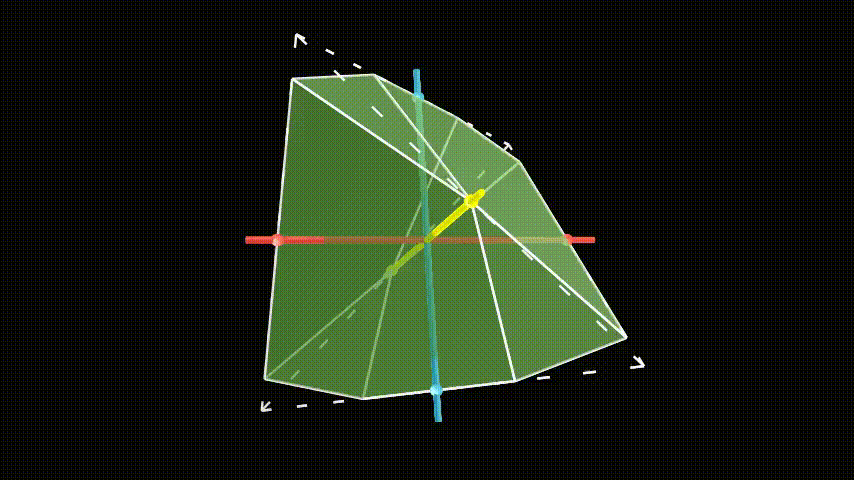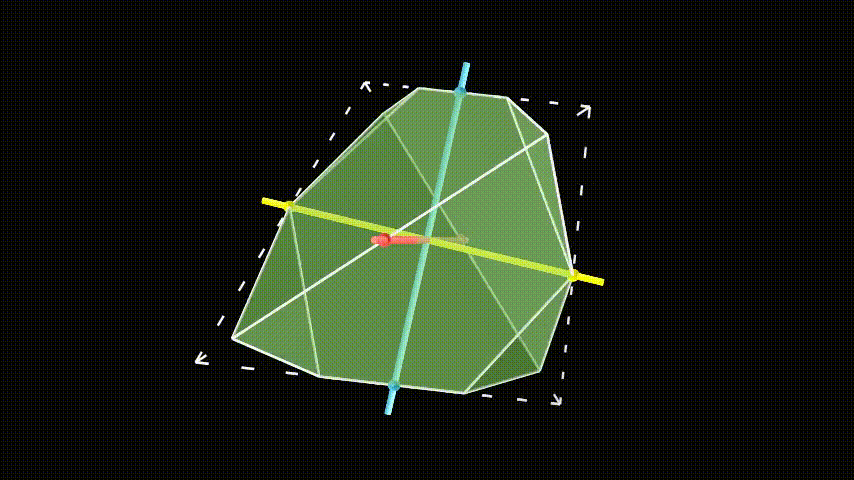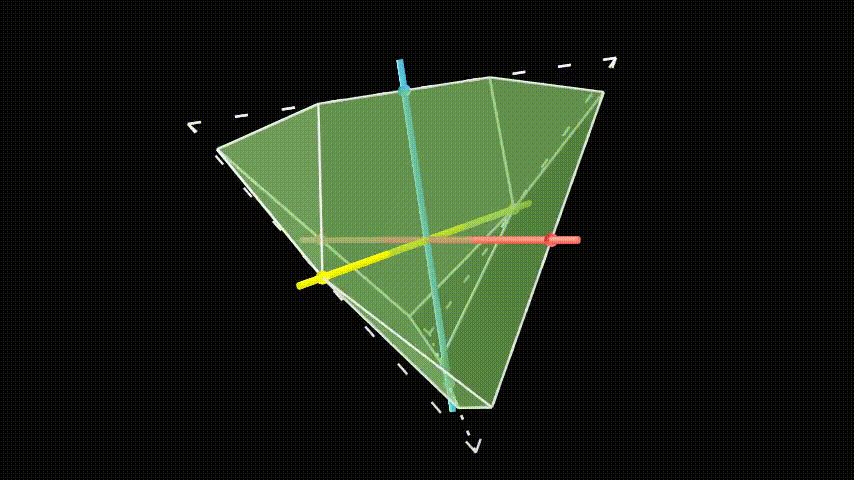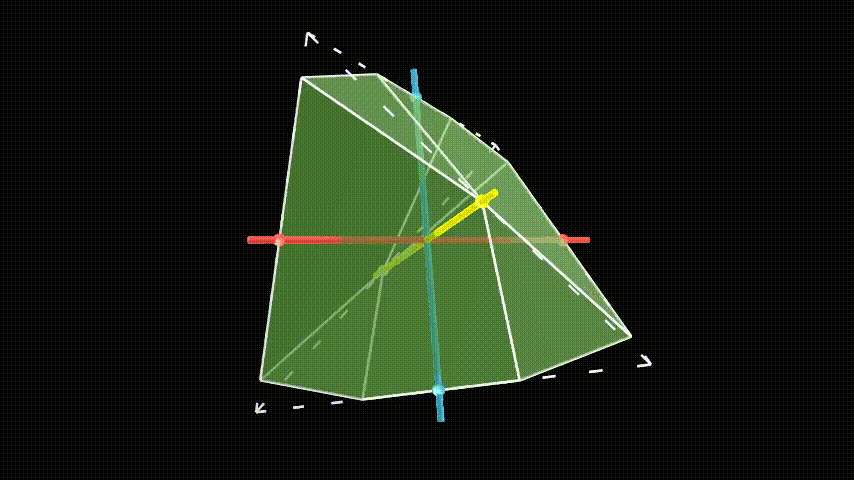
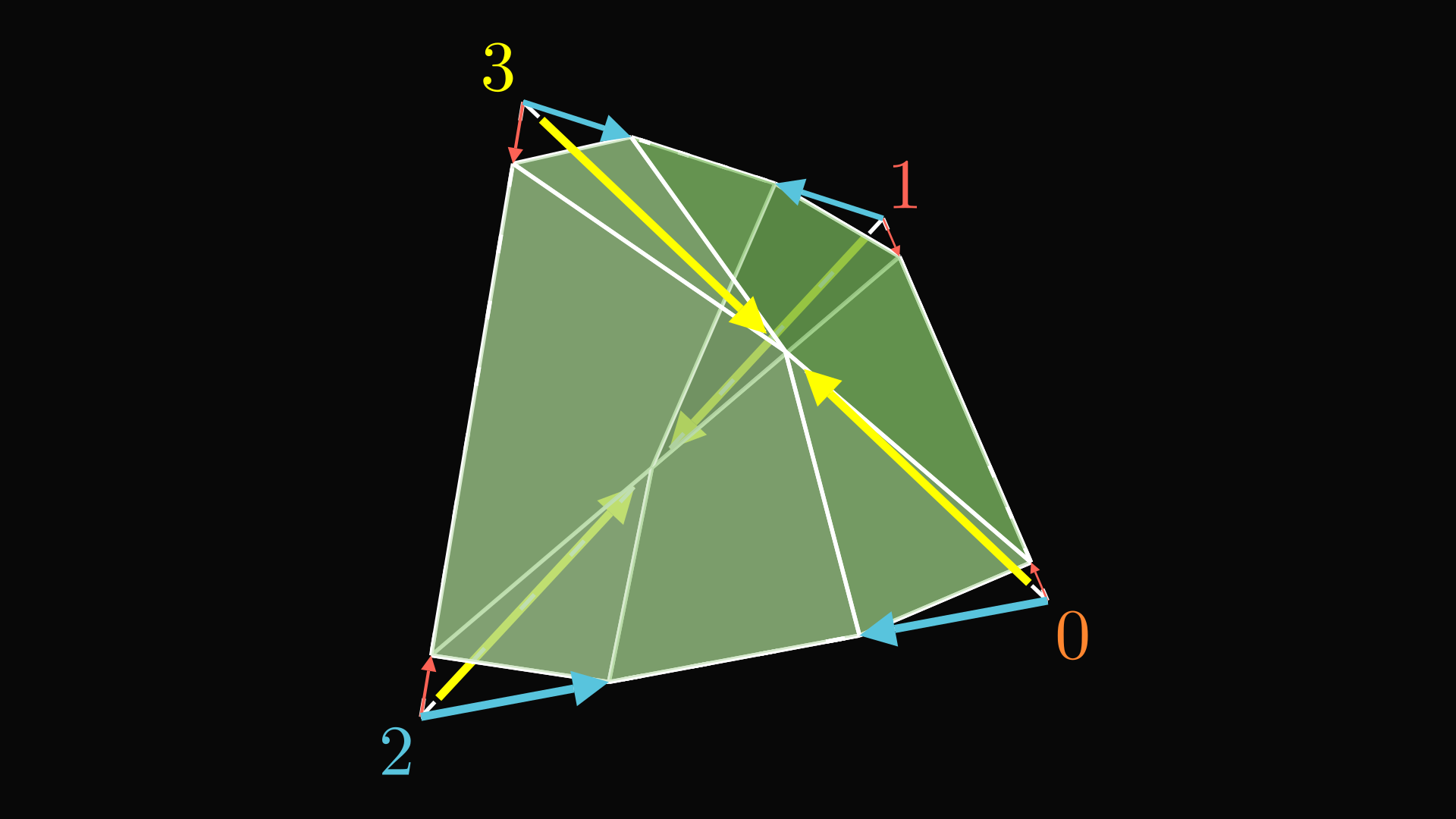
A simple way to destroy some of the symmetries of the object is to add some sort of asymmetrical decoration onto one of the vertices, say the one corresponding to the identity element. This makes any transformation that leaves this vertex in a different orientation illegal. A simple decoration is an asymmetrical notch taken out of the vertex, which works in any dimension.
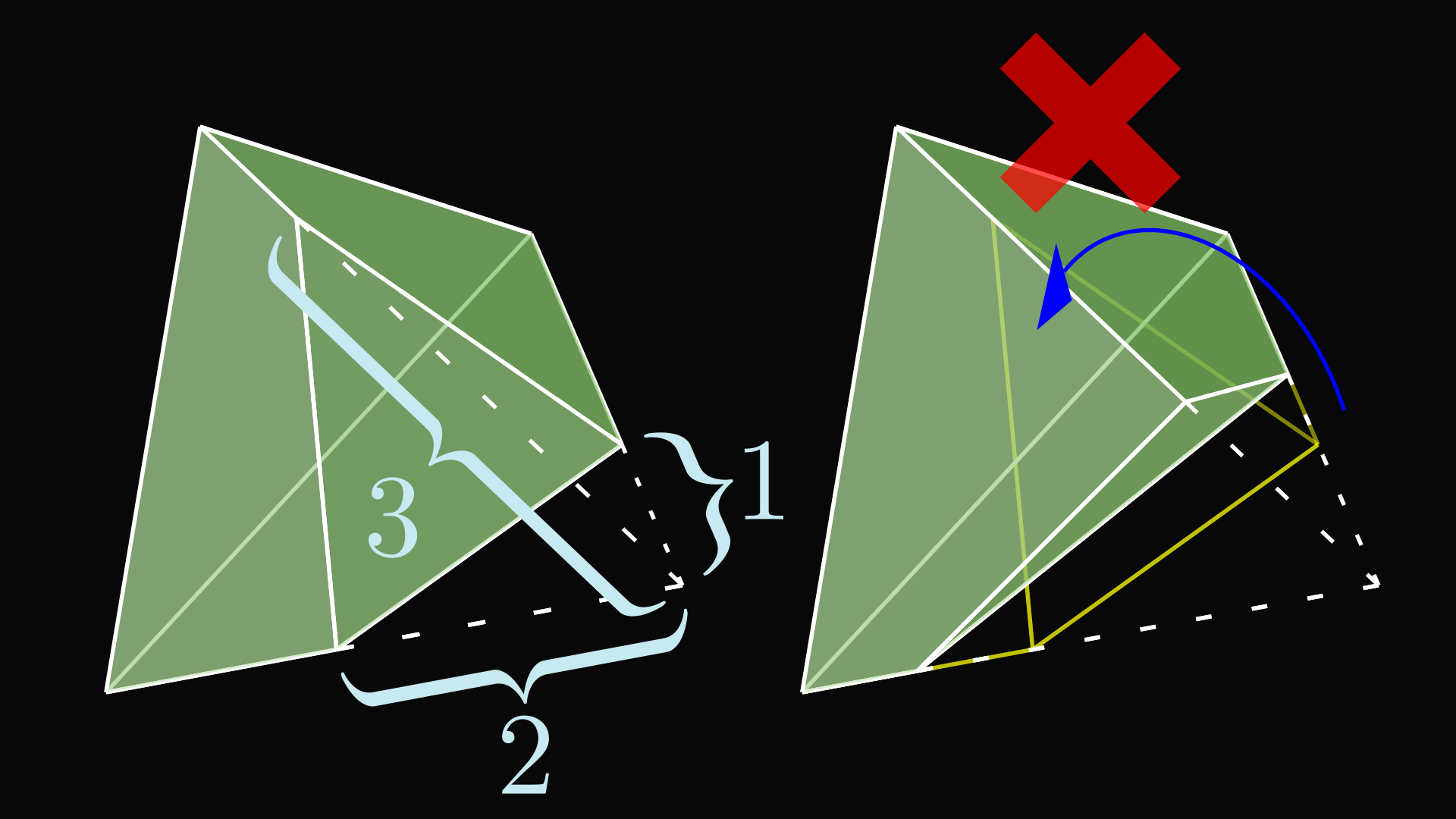
We still need to allow the symmetries that take the decorated identity vertex to a different vertex. This means we have to copy this decoration to the other vertices. When we apply all of the transformations, the identity vertex will visit each vertex once, and we copy the decoration in whatever orientation it ends up. (The long sides of the notches don’t have to touch each other, it just looks prettier.)
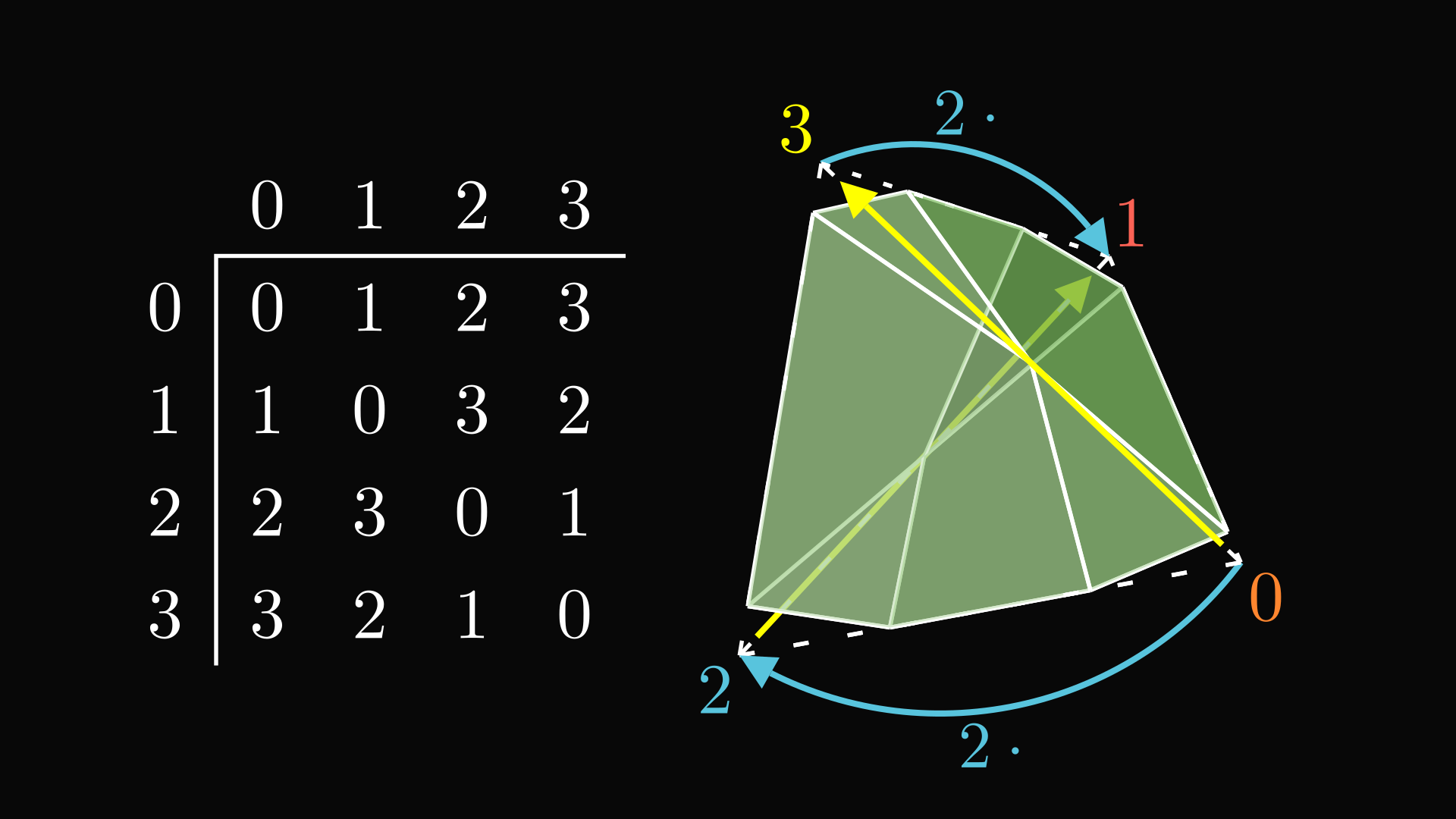
For instance, the notch on the identity vertex (0) has its long, pointy side pointed towards vertex 3. If we perform transformation 2, the identity vertex goes to vertex 2·0=2. Then we copy the notch onto vertex 2 in the same orientation it goes under transformation 2. Under transformation 2, vertex 3, where the long side of the identity decoration pointed, goes to vertex 2·3=1, so the long side of the notch at vertex 2 has to point at vertex 1.
Because every vertex now has an asymmetrical decoration, this shape has no symmetries other than the ones corresponding to the elements of the group. However, we might have destroyed some symmetries of the shape which we were supposed to keep. For instance, what if transformation 2 takes 3’s decoration to vertex 1, but in a different orientation than 1’s decoration was? That would invalidate that transformation.
Thankfully, this is not the case. Remember that each symmetry of the object corresponds to an element of the group, and doing two transformations, one after the other, corresponds to the group operation. 1’s decoration looks like 0’s decoration under the transformation 1. 3’s decoration looks like 0’s decoration under the transformation 3. Then if we transform 3’s decoration by 2, it will look like 0’s decoration transformed by 3 and then 2. This is the same as the transformation 2·3 (remember that function composition goes right to left). But that’s just transformation 1. So when vertex 3 is sent to vertex 1 under transformation 2, it looks like the old vertex 1. So this is still a valid symmetry.
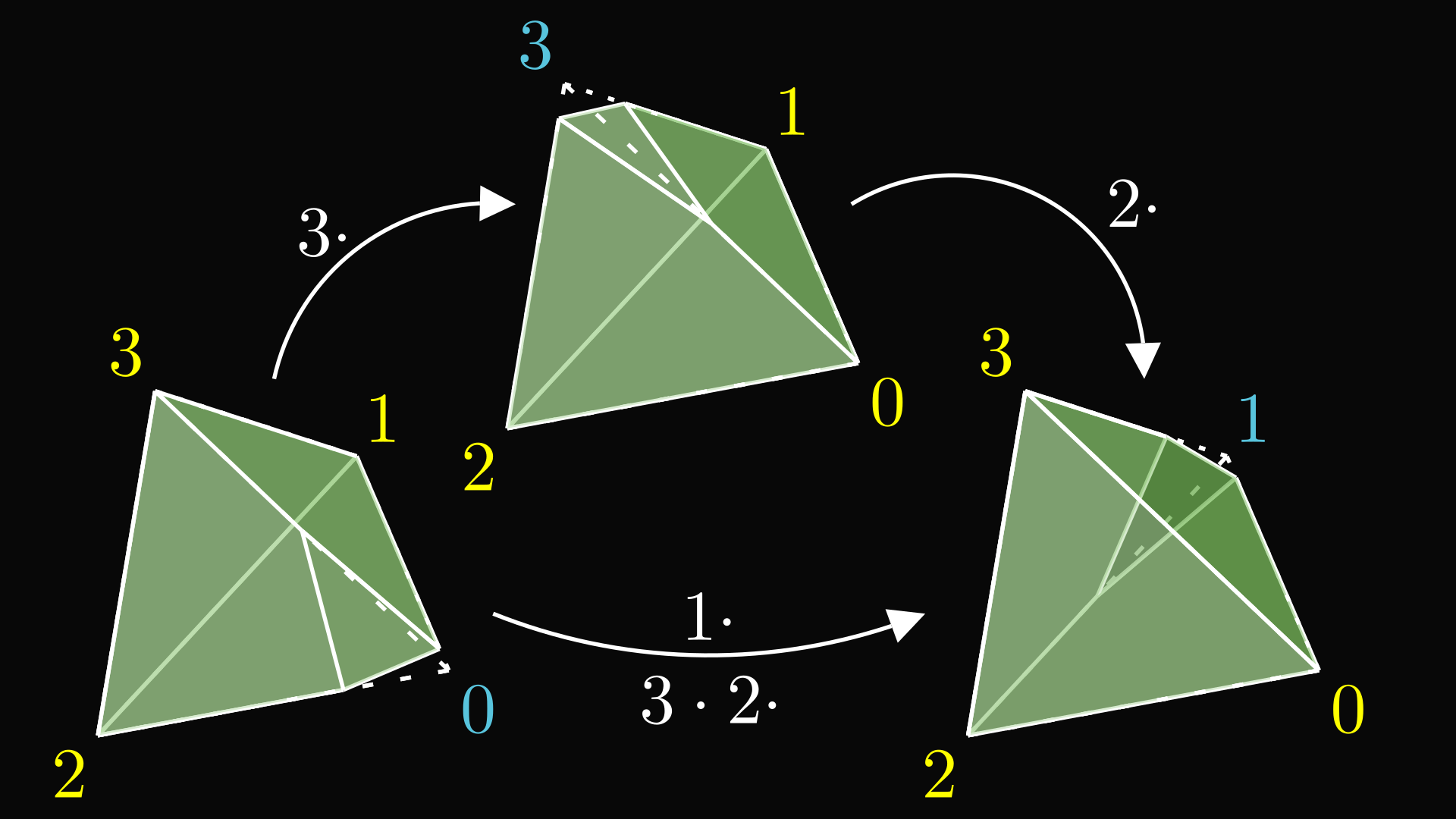
This means that every element of the group corresponds to a symmetry of the object. That symmetry permutes the vertices like the element permutes the other elements of the group under left-multiplication. Also, the object has no other symmetries besides the ones corresponding to the group. Third, doing two symmetries of the object one after another behaves exactly like multiplying their corresponding group elements. This makes our special object a perfect representation of the group: its symmetry group is exactly the group we were after.
This construction is from this Math Overflow thread, specifically the responses from Anton Geraschenko and Sergei Ivanov.
There are a few things to note about this construction. First, it doesn't always give you the simplest object with that symmetry group: the one with the fewest dimensions. In the example we’ve been using, the Klein four-group has 4 elements, so this construction uses a simplex of 4-1=3 dimensions. However, the Klein four-group has a simpler representation of only 2 dimensions: a non-square rhombus (or a non-square rectangle). Determining the object that represents a certain group with the least possible dimensions is much harder.
One interesting application of this puzzle has to do with the Monster group: the largest of a certain type of fundamental group called sporadic simple groups. This group has a simplest representation in 196 883 dimensions (over the field of complex numbers instead of the reals, but it’s very similar). This is suspiciously close to 196 884, a number that plays a role in modular function theory. This led to the “Monstrous moonshine” conjectures, which helped find links between modular functions and groups.
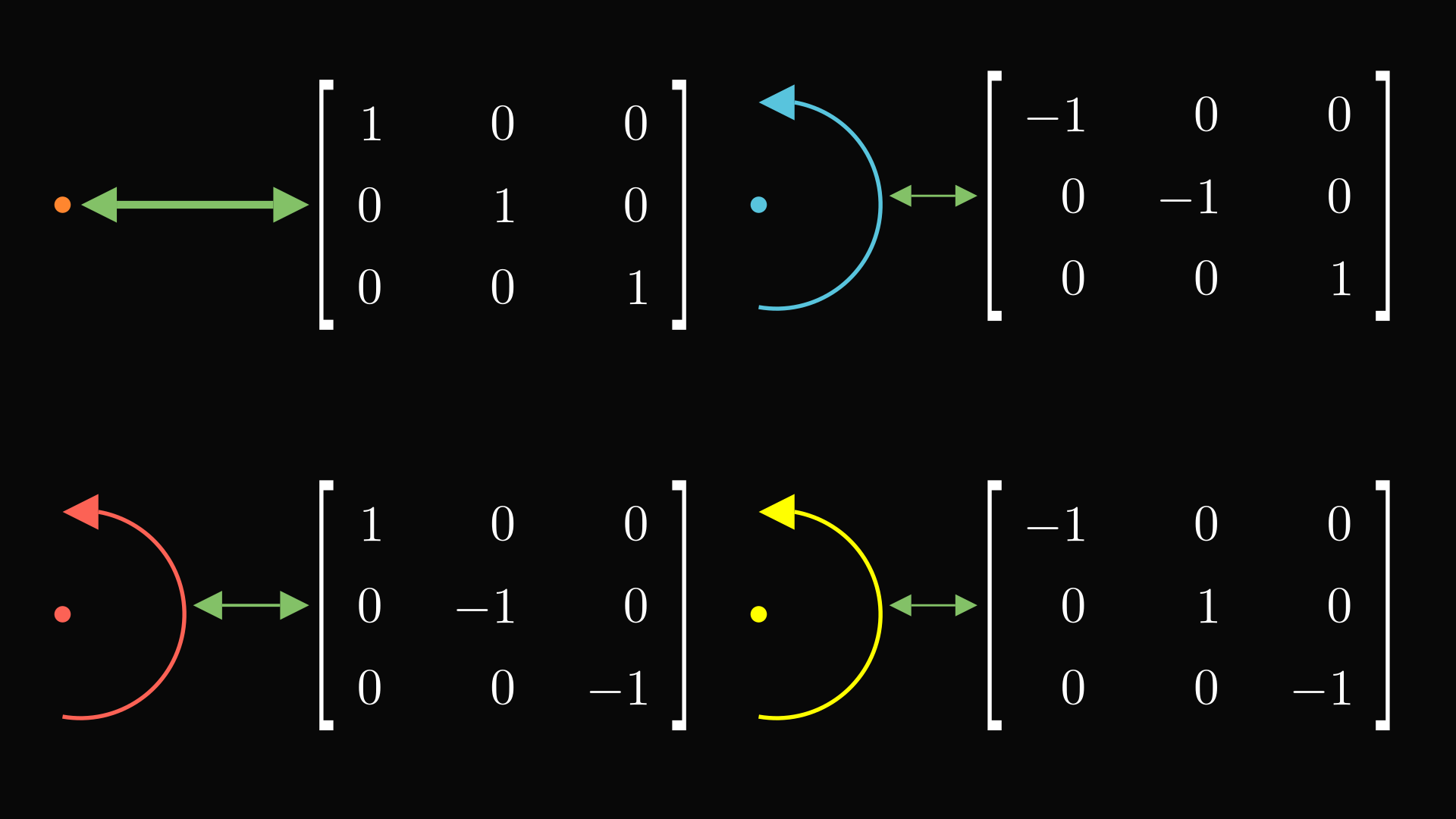
Each rotation of the object can be represented by a square matrix. These are easy to store and simple to compose. And, if you find a small set of generators for the group, and perhaps a lower dimension representation, they can be a very compact way to present the group.
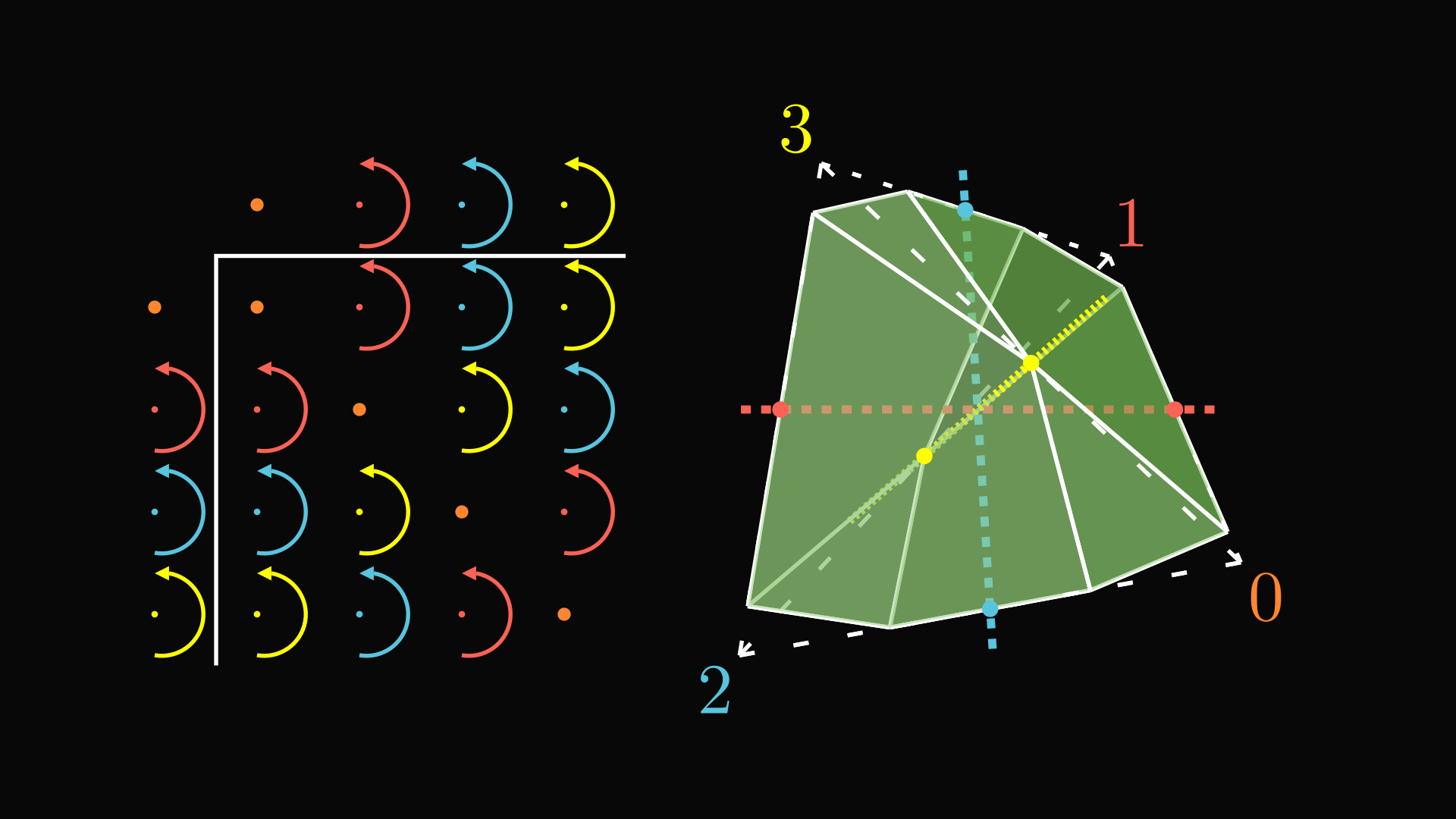
It can also be enlightening to study what the edges of this object look like. The long side of the notch at the identity vertex arbitrarily pointed at vertex 3. We can say the equation 0·3=3 corresponds to the fact that 0’s long notch side points at vertex 3. In other words, the long side of the notch is like an arrow telling you what you get if you multiply 0 by 3. The other vertices also have their long sides of the notches pointing at what you get when you multiply them by 3. The other sides of the notch correspond to multiplying by 1 and 2.
We can turn these arrows into a graph called the Cayley graph of the group. Each group element corresponds to a vertex, and each non-identity element gets a color. You draw arrows corresponding to how those elements transform the other elements of the group under the group operation. For instance, there is a yellow arrow from 1 to 2 because yellow means 3 and 1·3=2.
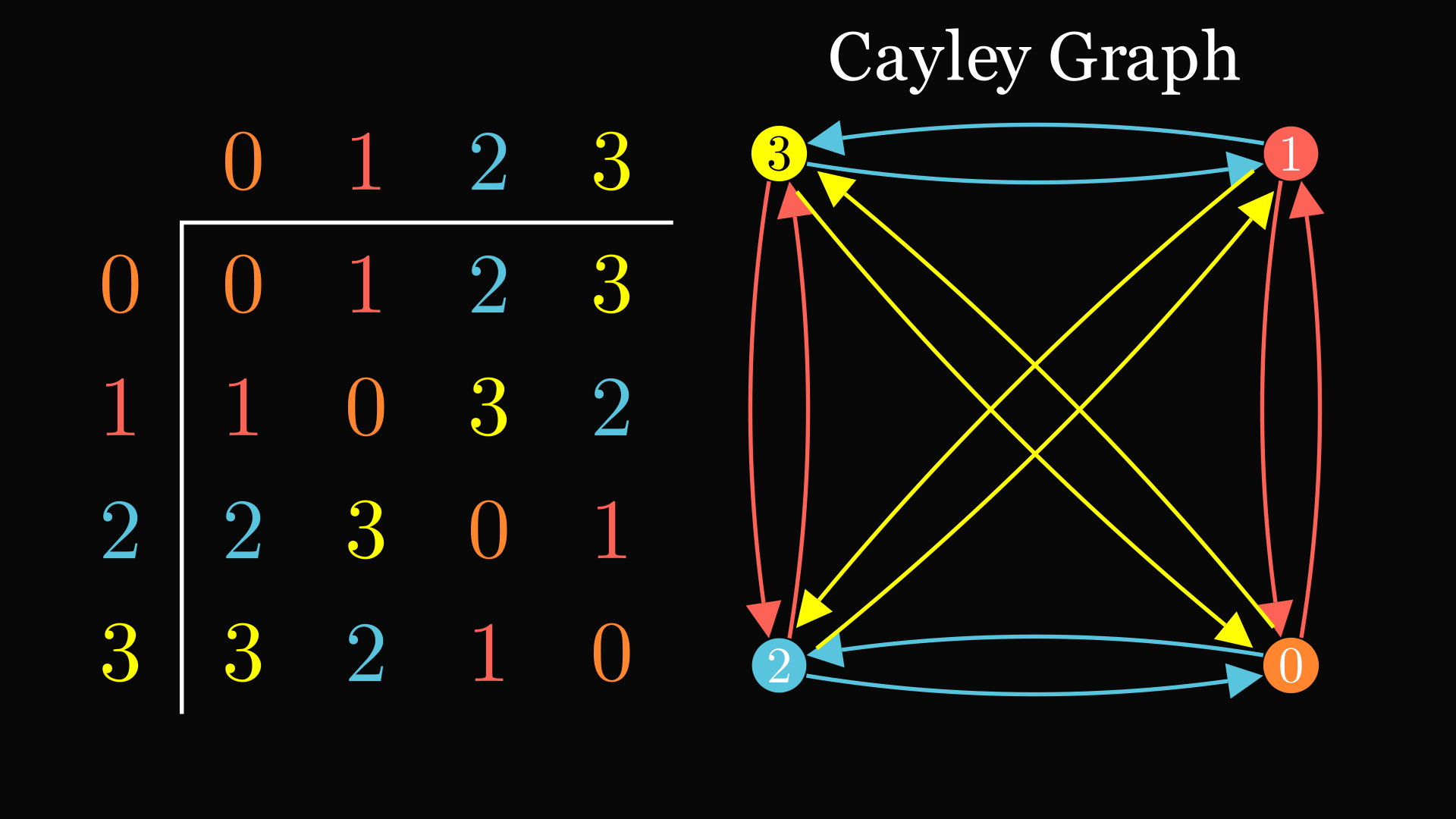
If we respect the colors and direction of the arrows, this graph actually has an automorphism group of the group in question. The automorphism group of a graph is basically its symmetry group, the group of all the ways to permute the vertices that leave edges where they should be. The asymmetrical colors of the arrows coming out of each vertex are like the asymmetrical notches on the object, which break all symmetries but the ones we want. All the symmetries corresponding to group elements are still allowed because of the way the colors are chosen, similar to the way the orientation of the decorations was chosen above. The associativity property is important for this.
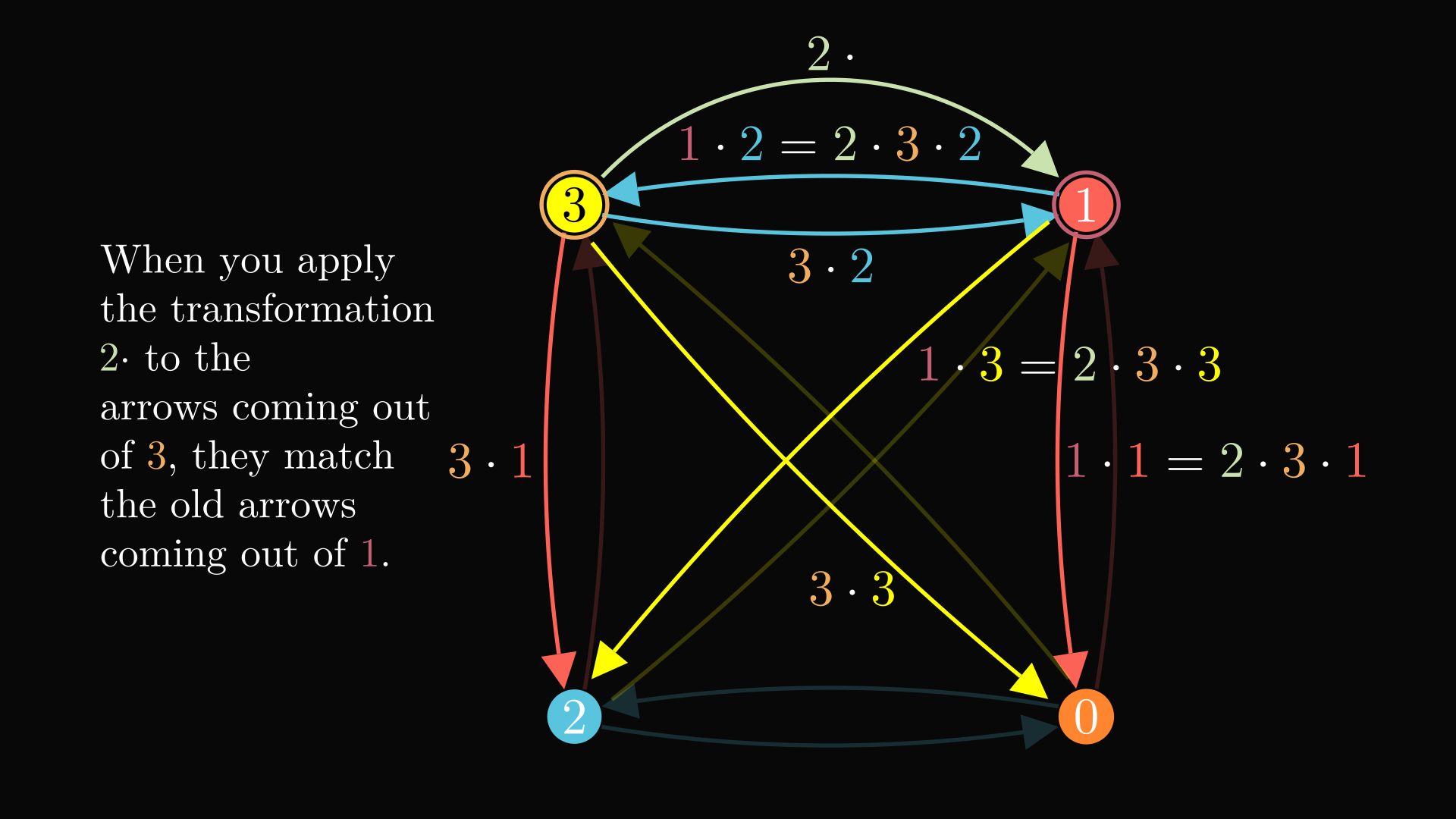
There are many other representations you can get of the group from the fact that G’s Cayley graphs’s symmetry group is G. For instance, you can turn this coloured, directed graph into a simple graph by turning the arrows into paths of different lengths. This simple graph still has the symmetry group of G. This leads to Frucht’s theorem, which says that every group has a graph with that symmetry group.
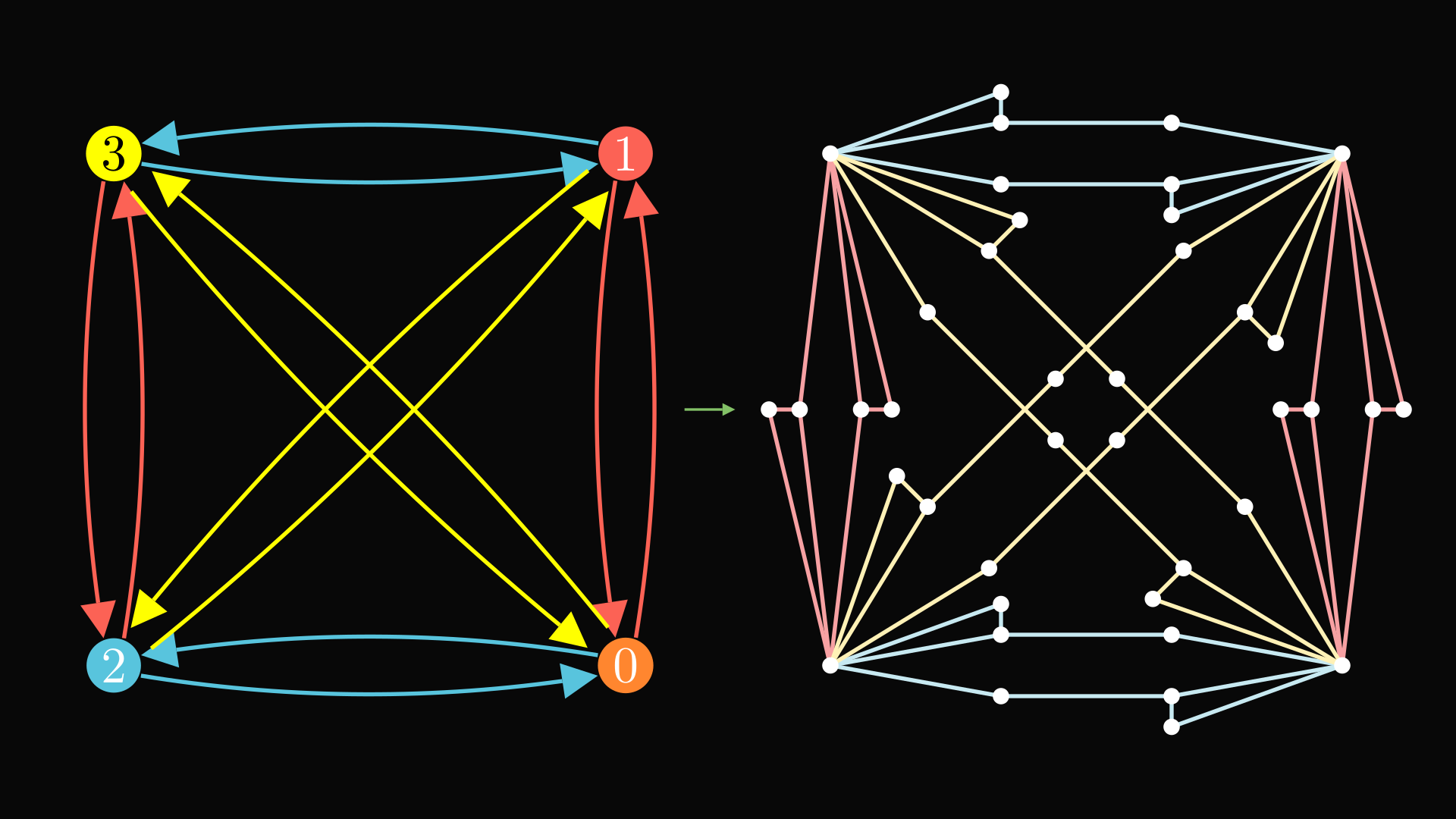
You can use Fruct’s theorem to create another construction of a polytope with a symmetry group of G. I’ll leave you to think of how. Hint: think back to what the symmetries of the simplex are, and what the symmetry group of a graph means.
Groups are incredibly abstract objects. They can sometimes be hard to wrap your mind around. Representations are ways to associate the elements of the group with some easier object, while keeping the structure of the group. For example, we have represented the Klein four-group with a rhombus and a 3D notched tetrahedron which both have the group as their symmetry group. Those symmetries can also be represented as a set of rotation matrices, which makes them very easy to store and compose. We can also represent the group with a Cayley graph, which is coloured and directed, or even a simple, uncoloured, undirected graph. There are many other useful ways to represent groups, and I hope this discussion has made you more comfortable with these important but intimidating objects.
Sources:
Information about Cayey's Theorem
Notched tetrahedron construction
Construction of graph in Frucht's theorem
Pictures created with Manim community edition
Entry for SoME2
Thanks for reading!